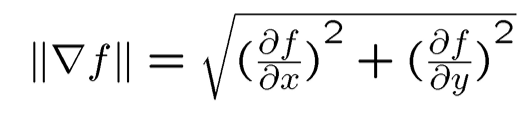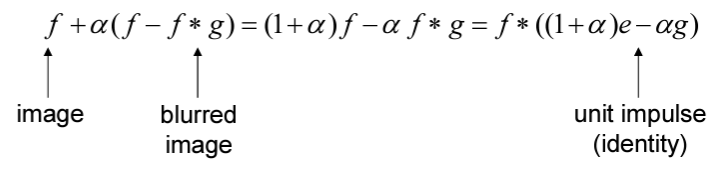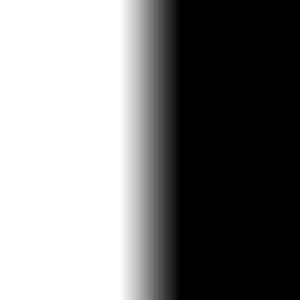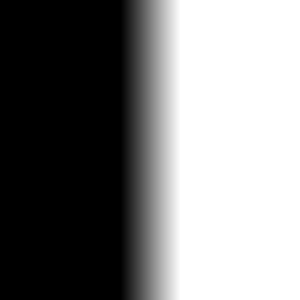Part 1.1: Finite Difference Operator
Include a brief description of gradient magnitude computation:
To get the gradient of the image, we first have to realize we are taking convolution in
two directions. The first direction Dx = [1, -1] while the second direction Dy = [[1], [-1]].
When we convolve the image with these kernel, we would get the following results.
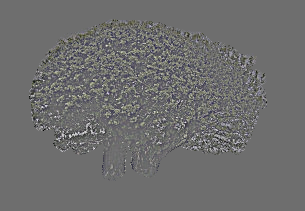
Then using the magnitude function (sum(square dx + square dy) then square root) we can find the gradient magnitude as shown.
Lastly, we will also threshold the magnitude image to reduce noises.